

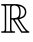

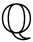






 が集合
が集合 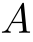 に属する」
に属する」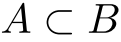
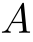 が集合
が集合  に含まれる」
に含まれる」
 の閉区間
の閉区間 

 の開区間
の開区間 
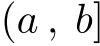
 の区間
の区間 
 ,
, 
 ,
,

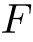 .
.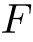 の最大値
の最大値 
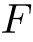 .
.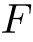 の最小値
の最小値 



 を
を 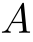 と呼ぶことにする.
と呼ぶことにする.
 座標 (
座標 ( 座標 of P)
座標 of P)
 .
.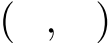
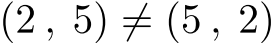 .
.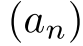
 だが
だが
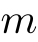 は
は  を割り切る.
を割り切る.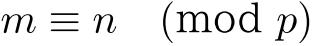
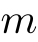 ,
,  は
は  で割った余りが等しい
で割った余りが等しい
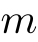 と
と  の最大公約数
の最大公約数
| 問題のの前で,考え方の糸口,目の付け所を | |
| 問題のの前で,解き方の方向性,大雑把な流れを | |
| 問題のの前で,解答用紙には書かないけれど 着想を得るために行う作業 | |
| 問題のに先立ち,そこで用いる根本的な考え方 | |
| 試験で,実際に解答用紙に書くこと. 補助説明は,赤字の吹き出しで | |
| とは違った解き方.試験での「答案」という体裁を取らず, 内容を大雑把に書いていることが多い. | |
| における主要な考えをより詳しく | |
| に対するちょっとした疑問を解消 | |
| 当該問題のからは少し外れる関連事項 | |
| 関連をもつさらに高度な内容.が付されている場合は,輪を掛けて高度 | |
| 文字通り:重要なこと | |
| 常套手段的内容.ただし,例外もあるかも | |
| 陥りがちな過ち,盲点の指摘 | |
| 内容に厳密性を欠いたり,前提とする条件に無理があったり, 申し訳なさを感じる際に | |
| 文字通り:具体例 | |
| 例えば,・~・・~~・・・, とあれば, ここまででは「終了」という意味 | |
| ハイレベルな内容 | |
| 必須度の高い内容 | |
| 必須度の低い内容 | |
| 理系生限定(数学Ⅲ範囲)の内容 | |
| 定義,基本原理(的な)内容.完璧に頭に刻み込む. | |
| 定理,問題解法(的な)内容.結果を記憶したい. | |
| 上記を入試で証明抜きに使ってよい. (だたし,定理の証明そのものが要求されている場合は別.) | |
| たぶん,上記を入試で証明抜きに使ってよい. | |
| 上記を入試で証明抜きに使ってよいか微妙.状況次第 | |
| 上記を入試で証明抜きには使えないのが原則 |
 レベルについて
レベルについて 必須度について
必須度について  | 複素数全体の集合. 手書きでは  |
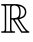 | 実数全体の集合.手書きでは  |
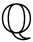 | 有理数全体の集合.手書きでは  |
 | 整数全体の集合.手書きでは  |
 | 自然数全体の集合.手書きでは  |
 | 「要素  が集合 が集合 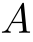 に属する」 に属する」 |
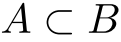 | 「集合 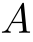 が集合 が集合  に含まれる」 に含まれる」 |
区間  |  の閉区間 の閉区間  |
区間  |  の開区間 の開区間  |
区間 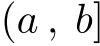 |  の区間 の区間  |
 , ,  |  , , |
 | maximal 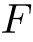 . .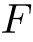 の最大値 の最大値 |
 | minimal 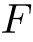 . .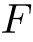 の最小値 の最小値 |
 | 「ゆえに」 |
 | 「なぜならば」 |
 | 「換言すれば」 |
 |  を を 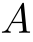 と呼ぶことにする. と呼ぶことにする. |
| □ | 「証明終わり」 |
 | 点 P の  座標 ( 座標 ( 座標 of P) 座標 of P) |
 | 順序を区別しない集まり=組合せ,集合. . . |
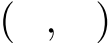 | 順序を区別する集まり=順列,組. 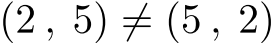 . . |
数列 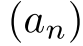 | 高校教科書では  だが だが |
| even | 偶数 |
| odd | 奇数 |
 | 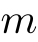 は は  を割り切る. を割り切る. |
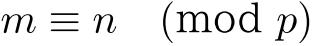 | 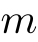 , ,  は は  で割った余りが等しい で割った余りが等しい |
 | 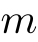 と と  の最大公約数 の最大公約数 |
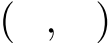 」は,「開区間」「順列」「最大公約数」の 3 通りの意味で使われる.文脈の中で,どの意味かが混同されそうな場合には,「区間
」は,「開区間」「順列」「最大公約数」の 3 通りの意味で使われる.文脈の中で,どの意味かが混同されそうな場合には,「区間 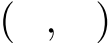 」,「組
」,「組 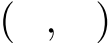 」,「最大公約数
」,「最大公約数 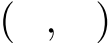 」などと言葉を添えるべし.
最大公約数に関しては,その場で「
」などと言葉を添えるべし.
最大公約数に関しては,その場で「 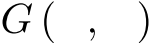 と表す」などと誤解の生じない記号を宣言をして使うのもよい.
と表す」などと誤解の生じない記号を宣言をして使うのもよい.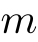 ,
,
 ,
,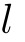
 ,
,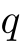 ,
,
 ,
,
 ,
, ,
, ,
, ,
,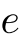
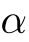 |
 |
 |
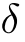 |
 |
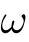 |
| アルファ | ベータ | ガンマ | デルタ | イプシロン | オメガ |
 |
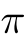 |
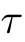 |
 |
 |
 |
| ラムダ | パイ | タウ | シータ | ファイ | プサイ |