用語一覧
- 各用語の意味がもっとも詳しく書かれているページへのリンクが張ってあります.
- 用語の中で,意味が分かりにくいもの,バッド・ネーミングされたもの,誤解を招きやすいものには「」マークを付しました.
,最後に「イミ不明単語」としてまとめました.
- 各用語には,よみがなと英訳(アクセント記号付き)が付してあります.
あ
か
さ
た
な
は
ま
や
ら
わ
記号
意味不明語
op
[あ]
- 余り (整数の除法についての)
remáinder
-
整数の除法での等式:
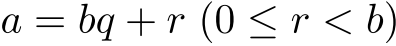 における
における  のこと.
のこと.
- 一意
uníque
- ただ1つに.
- 一般項
géneral term
- 数列の第
 項を,その番号
項を,その番号  で表したもの.
で表したもの.
- 因数定理
fáctor théorem
-
「整式
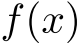 が
が  で割り切れる」⇔
で割り切れる」⇔ 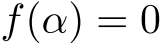 .
.
- 裏
invérse
-
命題:「(c) ⇒ (a)」の「裏」とは,両条件の否定から作られる「
 ⇒
⇒ 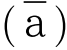 」のこと.
」のこと.
-
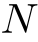 進法
N-ary notation
進法
N-ary notation
-
2以上の整数「
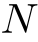 」を基にし, 各位を表す数として 0 ~
」を基にし, 各位を表す数として 0 ~  を用いる位取り記数法.
を用いる位取り記数法.
- オイラー関数
Euler's tótient fúnction
-
1 から
 までの整数の中で,
までの整数の中で, と互いに素であるものの個数.「
と互いに素であるものの個数.「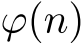 」と表すことが多い.
」と表すことが多い.
op
[か]
- 階差数列
dífference séquence
-
 を,数列
を,数列 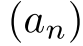 の階差数列という.(本書では,単に「隣どうしの差」の意味で,「
の階差数列という.(本書では,単に「隣どうしの差」の意味で,「  」とかも階差数列,あるいは短く「階差」と呼んでいる.)「和」との関係が重要.
」とかも階差数列,あるいは短く「階差」と呼んでいる.)「和」との関係が重要.
- 階乗
factórial
-
1 から
 までの自然数の積:
までの自然数の積: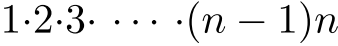 .記号:
.記号: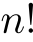 で表す.
で表す.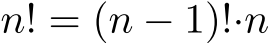 が成り立つ.
が成り立つ.
- ガウス記号
Gauss symbol
-
記号:
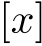 のこと.実数
のこと.実数  の整数部分,つまり,
の整数部分,つまり, を超えない最大の整数.
を超えない最大の整数.
- 関数
fúnction (表記 :
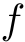 ,
, ,
,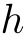 )
)
 から
から 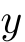 への一意的な対応.(「一意的」=「ただ1つ」)
への一意的な対応.(「一意的」=「ただ1つ」)- 完全数
pérfect númber
-
自然数
 の正の約数から自身を除いたものの総和が,
の正の約数から自身を除いたものの総和が, そのものと等しいとき,
そのものと等しいとき, を完全数と呼ぶ.
を完全数と呼ぶ.
- 奇素数
odd prime
- 奇数である素数:3 , 5 , 7 , 11 ,
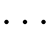 .つまり,2 (偶数)以外の素数.
.つまり,2 (偶数)以外の素数.
- 帰納 indúction
- 数学的な意味での「帰納」とは,数列を,初項と漸化式によって“ドミノ倒し”方式に捉える手法.ドミノ式に項を定めるのが「帰納的定義」,ドミノ式に命題を証明するのが「数学的帰納法」.ちなみに現代文における「帰納」とは,「有限個の観測データから一般法則を“類推”」する手法を指す,まったく別の意味の用語である.なお,対応する英単語:「induction」は,その語源(in=内,duct=導く)からわかるとおり,本来は上記現代文の方の意味をもつが,(英語圏の)数学の世界では,やはり上記数学的な方の意味で用いられる.つまり,英語の段階ですでに誤って使用されているのだ.迷惑至極である.(#^ω^)
- 帰納的定義
indúctive definítion
- 数列を,初項と漸化式によって“ドミノ倒し”方式で定める方法.
帰納
- 逆
convérse
-
命題:「(c) ⇒ (a)」の「逆」とは,矢印の向きを逆さにした「(a) ⇒ (c)」のこと.
- 共通部分
interséction
-
2 つの集合の両方に属する要素全体の集合.「交わり」と同義.
- 空集合
émpty set (表記 :
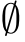 )
)
- 要素を 1 つも持たない集合.
- 位取り記数法
posítional notátion
-
十進法,2 進法などの
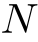 進法によって数を表す方法.
進法によって数を表す方法.
- 項 (数列の)
térm
- 数列を構成する1つ1つの数(または文字)
- 項 (整式の)
térm
- 整式を構成する1つ1つの単項式
- 公差
cómmon dífference
 (
( 
 1,2,3,
1,2,3, 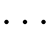 ) を満たす等差数列
) を満たす等差数列 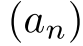 において,隣接項どうしの差
において,隣接項どうしの差  を
を 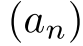 の公差という.
の公差という.- 格子点
láttice póint
-
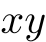 平面上で,両座標が整数である点.
平面上で,両座標が整数である点. 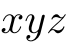 空間内での格子点も同様.
空間内での格子点も同様.
- 合成数
conpósite númber
-
2 個以上の素数の積で表される自然数.(例):
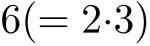 ,
, 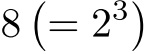
- 合同
congrúent
-
2 つの整数の余りが等しいこと.より正確には,差をとって得られる整数が割り切れること.
- 恒等式
idéntity
-
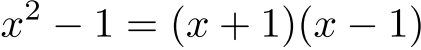 のように,全ての
のように,全ての  の値に対して両辺の値が等しくなるような等式.
の値に対して両辺の値が等しくなるような等式.
- 合同式
congrúence expréssion
-
2 つの整数が合同であることを表す式.
- 公倍数
common múltiple
-
2 つ(以上の)整数に共通な倍数.
- 公比
cómmon rátio
 (
( 
 1,2,3,
1,2,3, 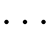 ) を満たす等比数列
) を満たす等比数列 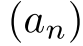 において,隣接項どうしの比
において,隣接項どうしの比  を
を 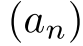 の公比という.
の公比という.- 公約数
cómmon devísor
-
2 つ(以上の)整数に共通な約数.
- 互除法
Euclidean álgorithm
-
「互除法の原理」を繰り返し用いて,2つの正整数の最大公約数を求める方法.
- 互除法の原理
mútual divísion
-
 のとき,最大公約数について
のとき,最大公約数について
 が成り立つこと.
が成り立つこと.
op
[さ]
- 最小公倍数
léast cómmon múltiple
-
公倍数の中で正で最小のもの.「L.C.M.」と略す.
- 最大公約数
gréatest cómmon devísor
-
公約数の中で最大のもの.「G.C.D.」と略す.
- 自然数
nátural númber
-
正の整数:
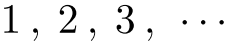 のこと.(大学以降では「0」も含める立場もある.)
のこと.(大学以降では「0」も含める立場もある.)
- 実数
real númber
- 実数は,「大きさ」をもち,数直線上の点と対応付けられる.
- 周期
périod
- 関数
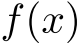 が,任意の
が,任意の  に対して
に対して 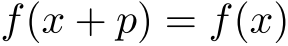 を満たす,つまり「
を満たす,つまり「  だけズレても同じ値をとる」ような 0 以外の定数.数列
だけズレても同じ値をとる」ような 0 以外の定数.数列 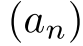 に対しても,
に対しても,  の関数とみなすことで同様な定義が適用できる.
の関数とみなすことで同様な定義が適用できる.
周期の中で「正で最小のもの」を「基本周期」というが,この「基本周期」のことを単に「周期」と言ってしまうこともあり,紛らわしい.文脈の中で判断せよ.
- 集合
sét(表記 :
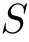 ,
, 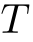 )
)
- ものの集まり.
- 十分条件
suffícient condítion
-
命題「(c) ⇒ (a)」が真であるとき,(c) は (a) であるための十分条件という.ただし,この用語を実際に使う際には,多くの場合別のニュアンスをもつ.
- 循環小数
repéating décimal
-
小数点以下において,同じ数の並びが繰り返される小数.
- 循環節
circulátion clause
-
循環小数において,繰り返される最短の列.
- 商 (整数の除法についての)
quótient
-
整数の除法での等式:
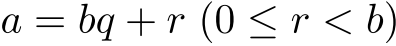 における
における 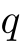 のこと.
のこと.
- 条件
condítion
- 文字を含んだ主張.その文字に何を代入するかで真偽が確定する.
- 小数部分
fráctional part
- 実数
 から,その整数部分
から,その整数部分 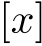 を引いた値
を引いた値 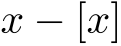 .
.
- 剰余系
compléte résidue system
-
余りの全種類を網羅した集合.(例):
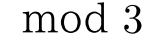 →
→ 
- 剰余類
résidue class
-
余りが等しい整数からなる集合.(例):
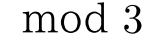 →
→ 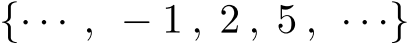
- 初項
first term
- その数列の中で初めの項,つまりもっとも番号
 が小さい項.数列
が小さい項.数列 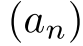 の場合,ふつうそれは
の場合,ふつうそれは 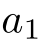 だが,
だが, 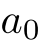 である場合などもある.
である場合などもある.
- 真理集合
truth set
- 文字
 を含んだ条件を真とするような
を含んだ条件を真とするような  全体の集合.
全体の集合.
- 数学的帰納法
mathemátical indúction
- 番号
 (
(  1,2,3,
1,2,3, 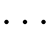 ) を含んだ無限個の命題を,“ドミノ倒し”方式で証明する方法.
帰納
) を含んだ無限個の命題を,“ドミノ倒し”方式で証明する方法.
帰納
- 数列
séquence
- 番号を付けて数(または文字)を並べたもの.
- 整式
polynómial
- 単項式と多項式を総称して整式という.
- 整式の除法
divísion
-
整式
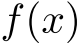 から整式
から整式 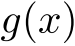 の整式倍を取り除いて
の形へ式変形すること.上記等式は,
の整式倍を取り除いて
の形へ式変形すること.上記等式は,  についての恒等式である.
についての恒等式である. 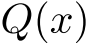 ,
, 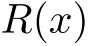 を,それぞれ「商」「余り」という.
を,それぞれ「商」「余り」という.
- 整除する
devisible
-
整数が整数を割り切ること.
- 整数
ínteger
-
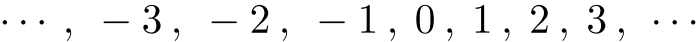 のような数.
のような数.
- 整数部分
íntegral part
-
実数
 を超えない最大の整数.ガウス記号:
を超えない最大の整数.ガウス記号: 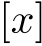 で表す.
で表す.
- 整数値多項式
ínteger-válued polynómial
-
多項式
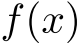 で,全ての整数
で,全ての整数  に対して
に対して 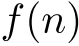 が整数となるもの.
が整数となるもの.
- 整数の除法
divísion
-
整数
 に対して,
に対して,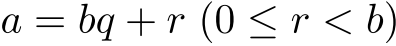 の形の等式を作ること.
の形の等式を作ること. 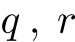 を,それぞれ「商」「余り」という.
を,それぞれ「商」「余り」という.
- 漸化式
recúrrence relátion
- 数列において,隣接項の間に成り立つ関係式.標準的な形は
 を
を 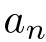 の式で表したものであるが,
の式で表したものであるが, 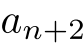 を
を  と
と 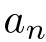 で表したものなどもある.
で表したものなどもある.
- 全体集合
univérsal set (表記:
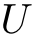 )
)
- 考察の対象としているもの全体からなる集合.
- 素因数
prime fáctor
-
素数である約数.
- 素因数分解
prime factorizátion
-
1 以外の自然数を,素数の積で表したもの.
- 属する
〔例〕
 is in
is in 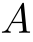
- ものが集合の要素であることを意味する.
- 素数
prime númber
- 正の約数をちょうど 2 つもつ自然数:2 , 3 , 5 , 7 , 11 ,
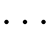 .1 は素数ではない.
.1 は素数ではない.
op
[た]
- 対偶
contraposítion
-
命題:「(c) ⇒ (a)」の「対偶」とは,両条件を否定し,矢印の向きを逆さにした「
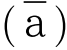 ⇒
⇒  」のこと.元の命題と真偽が一致する.
」のこと.元の命題と真偽が一致する.
- 互いに素
coprime
-
2 つの整数が共通素因数をもたないこと.つまり,最大公約数が 1 .
- 多項式
polynómial
-
単項式のいくつかを足して得られる式.高校教科書では項が 2 個以上の式を多項式としているが,単項式も含めた整式全体を,大学以降,および大学入試では多項式と呼ぶ.こちらの立場では,「整式」と「多項式」は同義語である.
- 単項式
monómial
- 数または文字を掛け合わせたもの.多項式を構成する1つ1つの項.
- 中国の剰余定理
Chinése remáinder théorem
-
連立合同方程式の解の存在を保証する定理.
- 等差数列
aríthmetic séquence
- 隣どうしの差が一定,つまり
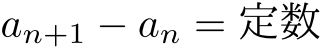 が全ての
が全ての  に対して成り立つ数列.
に対して成り立つ数列.
- 等比数列
geométric séquence
- 隣どうしの比が一定,つまり
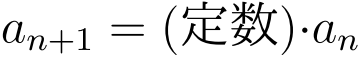 が全ての
が全ての  に対して成り立つ数列.
に対して成り立つ数列.
- “ドミノ式”
(俗な言い方)
-
数列を,第
 項(直前)と第
項(直前)と第  項(直後)の関係に注目してとらえる方法として本書では用いている.(割と幅広く使われている表現ですが.)
項(直後)の関係に注目してとらえる方法として本書では用いている.(割と幅広く使われている表現ですが.)
- ド・モルガンの法則
De Mórgan's laws
-
2 つの集合の交わり,結びの補集合について成り立つ法則.
op
[な]
- 二項係数
bínomial coeffícient
-
組み合わせの個数を表す
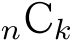 のこと.二項定理で展開した式の係数として現れるのでこう呼ばれる.
のこと.二項定理で展開した式の係数として現れるのでこう呼ばれる.
- 二項定理
bínomial théorem
-
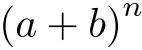 を展開する際に用いる.二項係数が現れる.逆に,二項展開した式を
を展開する際に用いる.二項係数が現れる.逆に,二項展開した式を 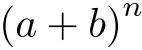 へ戻す,つまり因数分解するために用いることもある.
へ戻す,つまり因数分解するために用いることもある.
op
[は]
- 倍数
múltiple
-
整数の
 の整数倍を
の整数倍を  の倍数という.0 倍や
の倍数という.0 倍や 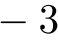 倍もある.
倍もある.
- 背理法
redúction to absúrdity
-
ある命題(P)を直接には証明しにくいとき,仮に「(P)でない」として矛盾を導くことによって「(P)である」ことを示す方法.
- はさみうち(俗称)
squéeze théorem
-
「
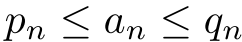 であり,
であり, 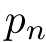 ,
, 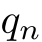 がともに
がともに 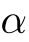 に収束するなら,
に収束するなら,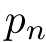 と
と 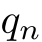 によって“はさまれた”
によって“はさまれた” 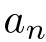 も
も 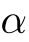 に収束する.」という「定理」.日本で“原理”と呼ぶ人が多いのは,単なる慣習.
に収束する.」という「定理」.日本で“原理”と呼ぶ人が多いのは,単なる慣習.
- ピタゴラス数
pythagoréan númber
-
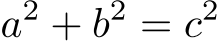 (「三平方の定理」=「ピタゴラスの定理」)を満たす自然数の組
(「三平方の定理」=「ピタゴラスの定理」)を満たす自然数の組 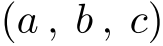 .
.
- 必要条件
nécessary condítion
-
命題「(c) ⇒ (a)」が真であるとき,(a) は (c) であるための必要条件という.ただし,この用語を実際に使う際には,多くの場合別のニュアンスをもつ.
- 否定
negátion
- ある条件と真偽が逆になる条件.
- フェルマーの小定理
Fermat's little théorem
 が素数,
が素数, が
が  と互いに素な自然数のとき,
と互いに素な自然数のとき, 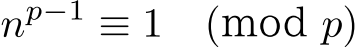 .
.
- 複素数
cómplex númber
- 実数
 と虚数単位
と虚数単位  を用いて
を用いて  と表される数.
と表される数.
- 不定方程式
indéfinite equátion
-
方程式の個数が,未知数の個数より少なく,解が定まらないもの.文字が「整数」であることを利用して解く問題がよくある.
- 部分集合
súbset
- ある集合の一部.
- 平方剰余
quadrátic résidue
-
平方数を割った余り.
- 平方数
squáre númber
-
ある整数を 2 乗して得られる整数:0 , 1 , 4 , 9 , 16 ,
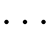
- 法
módulus
-
「
 を法とする」とは,合同式を用いる際に
を法とする」とは,合同式を用いる際に  で割った余りを考えること.
で割った余りを考えること.
- 包含関係
inclúsion relátion
- 2 つの集合の一方が他方の部分集合であること.
- 包除原理
inclúsion-exclúsion prínciple
-
和集合の要素の個数に関して成り立つ法則.
- 補集合
cómplement
- 全体集合から,ある集合の要素を除いてできる集合.
op
[ま]
- 交わり
interséction
-
2 つの集合の両方に属する要素全体の集合.「共通部分」と同義.
- 無限降下法
ínfinite descént
-
ある自然数から出発し,より小さな自然数を次から次へと作って 0 に近づけ,1 未満の自然数が存在するという矛盾を導く証明法.
- 無限小数
ínfinite décimal
-
桁数が無限である小数.
- 結び
únion
- 2 つの集合の少なくとも一方に属する要素全体の集合.「和集合」と同義
- 無理数
irrátional number
-
実数の中で,有理数ではないもの.
- 命題
proposítion (表記 :
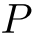 ,
, 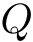 )
)
- 等式,不等式など,真偽が明確に定まる主張
op
[や]
- 約数
devísor
-
 (
( 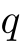 はある整数)のとき,
はある整数)のとき, は
は  の約数という.負の約数もある.
の約数という.負の約数もある.
- 有限小数
fínite décimal
-
桁数が有限である小数.
- 有理数
rátional number
-
ある整数
 の比の形:
の比の形: 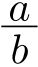 で表せる数.「ratio」=「比」なので,「有比数」と命名して欲しかった.残念・・・
で表せる数.「ratio」=「比」なので,「有比数」と命名して欲しかった.残念・・・
- 要素
élement
- 集合を構成する 1 つ 1 つのもの.
op
[ら]
- 連立合同方程式
élement
-
複数の合同式を満たす整数を求める問題.中国の剰余定理
op
[わ]
- 和 (数列の和)
sum (表記 :
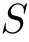 ,
, 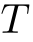 ,
, 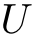 )
)
- 数列の指定された項の合計.「階差」
との関係が重要.
- 和集合
únion
- 2 つの集合の少なくとも一方に属する要素全体の集合.「結び」と同義
op
[記号]
- Σ記号
- 数列の和を表す記号
-
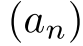
- 番号をつけて並んだ数列
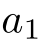 ,
, 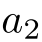 ,
, 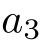 ,
, 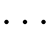 の名前.高校教科書では
の名前.高校教科書では  のように中括弧で記されるが,これは通常順序を無視した「集合」を表す記法であり,順序を区別した「数列」を表すのにはふさわしくない.
のように中括弧で記されるが,これは通常順序を無視した「集合」を表す記法であり,順序を区別した「数列」を表すのにはふさわしくない.
op
[意味不明語]
帰納
帰納的定義
数学的帰納法
多項式
有理数
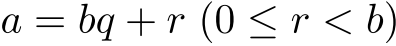 における
における  のこと.
のこと. 項を,その番号
項を,その番号  で表したもの.
で表したもの.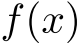 が
が  で割り切れる」⇔
で割り切れる」⇔ 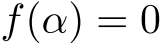 .
.
 ⇒
⇒ 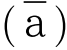 」のこと.
」のこと.
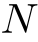 進法
N-ary notation
進法
N-ary notation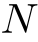 」を基にし, 各位を表す数として 0 ~
」を基にし, 各位を表す数として 0 ~  を用いる位取り記数法.
を用いる位取り記数法.
 までの整数の中で,
までの整数の中で, と互いに素であるものの個数.「
と互いに素であるものの個数.「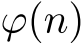 」と表すことが多い.
」と表すことが多い.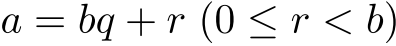 における
における  のこと.
のこと. 項を,その番号
項を,その番号  で表したもの.
で表したもの.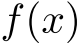 が
が  で割り切れる」⇔
で割り切れる」⇔ 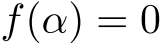 .
.
 ⇒
⇒ 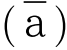 」のこと.
」のこと.
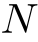 進法
N-ary notation
進法
N-ary notation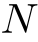 」を基にし, 各位を表す数として 0 ~
」を基にし, 各位を表す数として 0 ~  を用いる位取り記数法.
を用いる位取り記数法.
 までの整数の中で,
までの整数の中で, と互いに素であるものの個数.「
と互いに素であるものの個数.「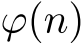 」と表すことが多い.
」と表すことが多い. を,数列
を,数列 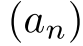 の階差数列という.(本書では,単に「隣どうしの差」の意味で,「
の階差数列という.(本書では,単に「隣どうしの差」の意味で,「  」とかも階差数列,あるいは短く「階差」と呼んでいる.)「和」との関係が重要.
」とかも階差数列,あるいは短く「階差」と呼んでいる.)「和」との関係が重要.
 までの自然数の積:
までの自然数の積: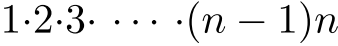 .記号:
.記号: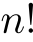 で表す.
で表す.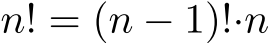 が成り立つ.
が成り立つ.
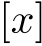 のこと.実数
のこと.実数  の整数部分,つまり,
の整数部分,つまり, を超えない最大の整数.
を超えない最大の整数.
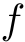 ,
, ,
,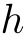 )
) から
から 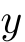 への一意的な対応.(「一意的」=「ただ1つ」)
への一意的な対応.(「一意的」=「ただ1つ」) の正の約数から自身を除いたものの総和が,
の正の約数から自身を除いたものの総和が, そのものと等しいとき,
そのものと等しいとき, を完全数と呼ぶ.
を完全数と呼ぶ.
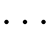 .つまり,2 (偶数)以外の素数.
.つまり,2 (偶数)以外の素数.
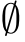 )
)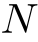 進法によって数を表す方法.
進法によって数を表す方法.
 (
( 
 1,2,3,
1,2,3, 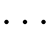 ) を満たす等差数列
) を満たす等差数列 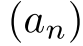 において,隣接項どうしの差
において,隣接項どうしの差  を
を 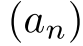 の公差という.
の公差という.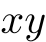 平面上で,両座標が整数である点.
平面上で,両座標が整数である点. 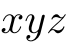 空間内での格子点も同様.
空間内での格子点も同様.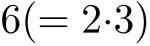 ,
, 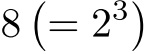
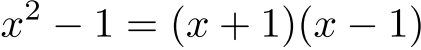 のように,全ての
のように,全ての  の値に対して両辺の値が等しくなるような等式.
の値に対して両辺の値が等しくなるような等式. (
( 
 1,2,3,
1,2,3, 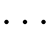 ) を満たす等比数列
) を満たす等比数列 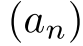 において,隣接項どうしの比
において,隣接項どうしの比  を
を 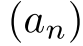 の公比という.
の公比という. のとき,最大公約数について
のとき,最大公約数について
 が成り立つこと.
が成り立つこと.
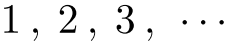 のこと.(大学以降では「0」も含める立場もある.)
のこと.(大学以降では「0」も含める立場もある.)
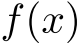 が,任意の
が,任意の  に対して
に対して 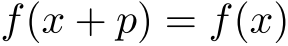 を満たす,つまり「
を満たす,つまり「  だけズレても同じ値をとる」ような 0 以外の定数.数列
だけズレても同じ値をとる」ような 0 以外の定数.数列 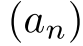 に対しても,
に対しても,  の関数とみなすことで同様な定義が適用できる.
の関数とみなすことで同様な定義が適用できる.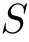 ,
, 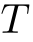 )
)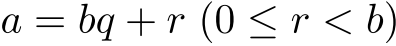 における
における 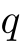 のこと.
のこと. から,その整数部分
から,その整数部分 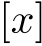 を引いた値
を引いた値 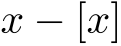 .
.
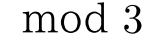 →
→ 
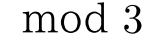 →
→ 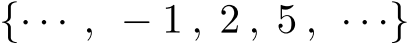
 が小さい項.数列
が小さい項.数列 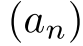 の場合,ふつうそれは
の場合,ふつうそれは 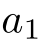 だが,
だが, 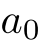 である場合などもある.
である場合などもある. を含んだ条件を真とするような
を含んだ条件を真とするような  全体の集合.
全体の集合. (
(  1,2,3,
1,2,3, 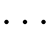 ) を含んだ無限個の命題を,“ドミノ倒し”方式で証明する方法.
帰納
) を含んだ無限個の命題を,“ドミノ倒し”方式で証明する方法.
帰納
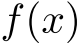 から整式
から整式 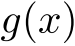 の整式倍を取り除いて
の整式倍を取り除いて
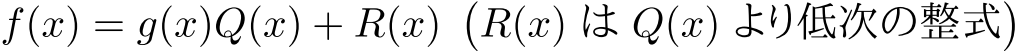
 についての恒等式である.
についての恒等式である. 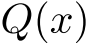 ,
, 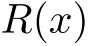 を,それぞれ「商」「余り」という.
を,それぞれ「商」「余り」という.
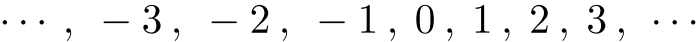 のような数.
のような数.
 を超えない最大の整数.ガウス記号:
を超えない最大の整数.ガウス記号: 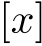 で表す.
で表す.
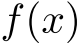 で,全ての整数
で,全ての整数  に対して
に対して 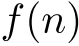 が整数となるもの.
が整数となるもの.
 に対して,
に対して,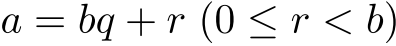 の形の等式を作ること.
の形の等式を作ること. 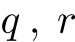 を,それぞれ「商」「余り」という.
を,それぞれ「商」「余り」という.
 を
を 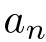 の式で表したものであるが,
の式で表したものであるが, 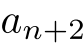 を
を  と
と 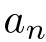 で表したものなどもある.
で表したものなどもある.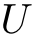 )
) is in
is in 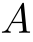
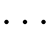 .1 は素数ではない.
.1 は素数ではない.
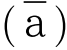 ⇒
⇒  」のこと.元の命題と真偽が一致する.
」のこと.元の命題と真偽が一致する.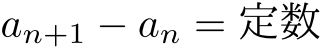 が全ての
が全ての  に対して成り立つ数列.
に対して成り立つ数列.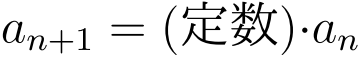 が全ての
が全ての  に対して成り立つ数列.
に対して成り立つ数列. 項(直前)と第
項(直前)と第  項(直後)の関係に注目してとらえる方法として本書では用いている.(割と幅広く使われている表現ですが.)
項(直後)の関係に注目してとらえる方法として本書では用いている.(割と幅広く使われている表現ですが.)
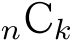 のこと.二項定理で展開した式の係数として現れるのでこう呼ばれる.
のこと.二項定理で展開した式の係数として現れるのでこう呼ばれる.
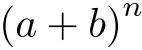 を展開する際に用いる.二項係数が現れる.逆に,二項展開した式を
を展開する際に用いる.二項係数が現れる.逆に,二項展開した式を 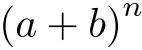 へ戻す,つまり因数分解するために用いることもある.
へ戻す,つまり因数分解するために用いることもある.
 の整数倍を
の整数倍を  の倍数という.0 倍や
の倍数という.0 倍や 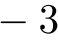 倍もある.
倍もある.
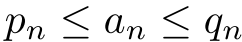 であり,
であり, 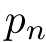 ,
, 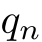 がともに
がともに 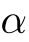 に収束するなら,
に収束するなら,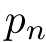 と
と 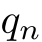 によって“はさまれた”
によって“はさまれた” 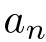 も
も 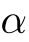 に収束する.」という「定理」.日本で“原理”と呼ぶ人が多いのは,単なる慣習.
に収束する.」という「定理」.日本で“原理”と呼ぶ人が多いのは,単なる慣習.
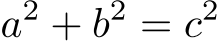 (「三平方の定理」=「ピタゴラスの定理」)を満たす自然数の組
(「三平方の定理」=「ピタゴラスの定理」)を満たす自然数の組 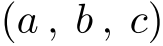 .
.
 が素数,
が素数, が
が  と互いに素な自然数のとき,
と互いに素な自然数のとき, 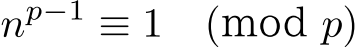 .
.
 と虚数単位
と虚数単位  を用いて
を用いて  と表される数.
と表される数.
 を法とする」とは,合同式を用いる際に
を法とする」とは,合同式を用いる際に  で割った余りを考えること.
で割った余りを考えること.
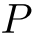 ,
, 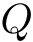 )
) (
( 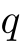 はある整数)のとき,
はある整数)のとき, は
は  の約数という.負の約数もある.
の約数という.負の約数もある.
 の比の形:
の比の形: 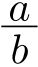 で表せる数.「ratio」=「比」なので,「有比数」と命名して欲しかった.残念・・・
で表せる数.「ratio」=「比」なので,「有比数」と命名して欲しかった.残念・・・
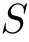 ,
, 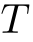 ,
, 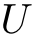 )
)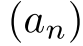
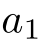 ,
, 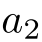 ,
, 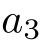 ,
, 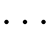 の名前.高校教科書では
の名前.高校教科書では  のように中括弧で記されるが,これは通常順序を無視した「集合」を表す記法であり,順序を区別した「数列」を表すのにはふさわしくない.
のように中括弧で記されるが,これは通常順序を無視した「集合」を表す記法であり,順序を区別した「数列」を表すのにはふさわしくない.